近年来,微创技术在齿槽外科的应用日益普及,但在复杂牙尤其是阻生牙的拔除术中,囿于传统拔牙原理 的限制,微创技术的运用并不彻底,使得手术创伤无法减小到最小程度。本文将从刚体力学基础原理出发,对牙拔除术的阻力及消除方法进行分析,为微创拔牙的临床操作提供参考。
传统拔牙技术中的力学原理和应用
传统拔牙技术中,为了让牙齿或牙根脱位,主要依靠压缩牙槽骨骨质、扩大牙槽窝来去除阻力而脱位。牙钳使用时颊舌向摇动即是为了达到这个目的。牙挺使用的力学原理,有杠杆原理、轮轴原理和楔的原理。这几个原理都是省力杠杆的原理,也就是达到术者用较小的力量获得对牙齿或牙根较大挤压和脱位的力量,使牙槽窝受挤压扩大,牙齿脱位。在此过程中,必然伴有较大的创伤。另外,对于无法钳夹和安放牙挺的残根、断根,为了减除阻力,往往需要去除较大量的骨质,从而造成骨质的创伤,术后常有较为严重的创伤反应。
近几十年来,各种牙槽外科的专著都涉及到了涡轮钻等牙科和外科动力系统在拔牙术中的应用。但多为结合具体案例的方法描述,对其中的力学原理的分析较为少见,故对于初学者常较难掌握。笔者在众多同仁的工作基础上对涡轮钻拔牙涉及到的拔牙力学原理进行了概括总结。
切割拔牙的微创力学原理
多数情况下,牙根是一个不规则椎体,牙槽窝的外形也与其相匹配,所以牙根要顺利脱位就需要克服牙槽窝的约束力,传统拔牙就是通过挤压牙槽窝,使牙槽窝骨壁变形、扩大,从而解除其对牙根的刚性约束。若牙槽窝不变形,则牙根就无法通过简单的移动或滑动来脱位。涡轮钻拔牙如果希望通过切割牙齿(根)的办法来解除其脱位的阻力,则力学原理就应遵从刚体力学原理。
刚体是指一个物体在运动中和受外力作用后,形状和大小不变,而且内部各点的相对位置不变的物体。可以把牙齿看作是一个刚体,把牙槽窝看成是刚性限制。绝对的刚体只是一种理想模型,因为任何物体在受力作用后,都或多或少有变形。牙槽窝骨质在牙拔除过程中很可能出现形变,如果变形的程度相对于物体本身的几何尺寸来说极为微小,那么,在研究物体运动时,其形变就可以忽略不计。通过合理的力学设计,让牙齿在脱位过程中尽量减小对牙槽骨的压力,将牙槽骨的形变控制在最小范围,就能达到微创的目的。而牙齿的无阻力或微阻力脱位,减小了颌骨的受力,同时也就保护了颞下颌关节和颈椎。
1.1 刚体平动与斜面原理
这个实际上是最简单的运动力学原理,物体O受到周围物体的抱持紧固而不易脱位,为了便于脱位,可以通过切割,人为地形成一个斜面,而沿着 这个斜面,A将非常容易脱位,斜面越大,内摩擦角α越小,阻力越小。而A脱位后,B就失去了周围组织的抱持紧固而易于脱位(图1)。具体操作时, 需要根据操作的可及性,灵活设计斜面的方向,必 要时可多次分牙。
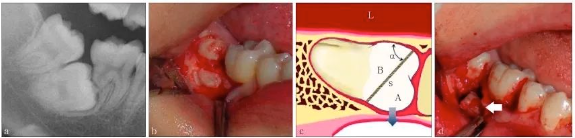
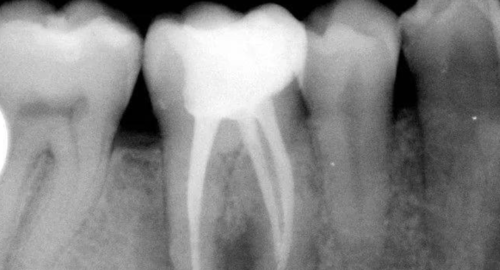
图 1 斜面原理
Fig 1 The slope principle
阻生的47已造成46远中牙根部分吸收(a),手术入路较为狭小而受限(b)。为了解除47脱位阻力,对牙体进行分割(c)。将47牙切割成A和B,A部分因斜面(s)的存在可沿蓝色箭头方向顺利脱位,并为B部分的松解创造空间,松解后的B部分可通过多次分割取出(d)。如此可以尽量减少开窗去骨量,多保留邻牙颈缘的骨质(白色箭头)。α:内摩擦角;L:舌侧。
1.2 榫楔原理
在中国传统木工和建筑中,为了紧固两个直角相交的部件,常常用到榫楔,以达到紧固的目的。在拔牙中,可以通过切割,形成一个“楔子”,然后先把“楔子”取出,这样两端的组织就容易脱位 了(图2)。
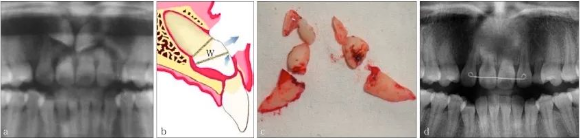
图 2 榫楔原理
Fig 2 The wedge principle
双侧阻生的上颌尖牙已导致双侧中切牙严重牙根吸收(a),为了避免在拔牙过程中对中切牙的挤压,分割牙体时,按图b中所示,将中间一段切割为上大下小的楔形(W),可以无阻力去除,然后再去除两端的牙体(c),从而在最大程度上保护了中切牙。在术后6月随访时,双侧中切牙已经稳固,其根尖部位骨质恢复良好(d)。
1.3 弧形差动原理
通常情况下,对于弯曲的牙根,前面所说的斜面原理和榫楔原理多无法起作用,这时真正能够利 用的是刚体运动学中的旋转运动原理。而非常有利的是,由于牙周膜的存在,使得牙槽窝对牙的限制 并不完全是刚性的。如果牙根弧度合适,器械可以 从其凸面进入,就可以较轻松地使其脱位,而不对牙槽窝形成明显的挤压(图3)。而有时,由于器械 (图3)只能从凹面进入,牙根脱位时就会遇到较大的阻力,从而需要通过进一步的切割,改变牙根脱位的运动轨迹,从而达到接近无阻力脱位的效果。
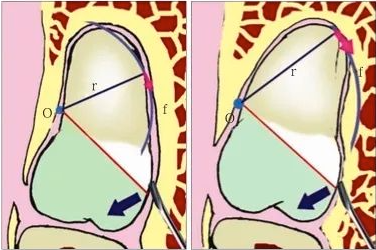
图 3 牙根弧形与脱位阻力
Fig 3 The relationship between the curve and dislocation of the root
由于牙根表面弧度不同,牙槽窝的弯曲弧度也不同,导致同样分牙后(绿色部分为先期去除的牙体组织),牙根脱位时阻力方向不同。左图中牙根脱位时,发生以O为旋转中心的圆周运动,阻力位点(f)脱位时,运动方向为箭头方向,可以顺利脱位。而在右图中,旋转中心(O)和旋转半径(r)一样的情况下,阻力位点(f)的脱位方向被牙槽窝阻挡,而不易脱位。
1.3.1 转动轴心与圆弧运动
这一原理在前倾或水平阻生智齿的拔除中运用最广。可以通过改变牙体转 动脱位时的运动轴心,来改变牙体上各点的运动方 向(图4),从而避开阻力而使牙齿脱位。但在此过程中,牙槽窝的挤压变形仍不可避免。尤其是舌 侧骨板的骨折,更是经常发生的事件。要进一步减 少对牙槽窝的挤压,则需要对牙根进行进一步的切割。
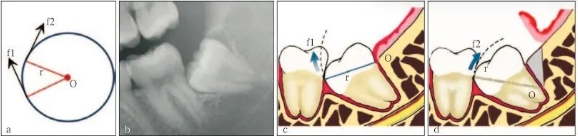
图 4 转动轴心与圆弧运动
Fig 4 The relationship between the centre and movement on the circle
在圆周运动(旋转)中,圆周上所有点的运动方向(f1、f2)均为切线方向,与通过该点的半径(r)相垂直(图a)。当牙齿发生旋转脱位时,其阻力点的运动方向会随着转动的轴心点的变化而变化,从而避开阻力。前倾阻生智齿(图b)脱位时,阻力分析如图c所示,因阻力点位于旋转中心(O)的下方,旋转脱位时,其阻力点的运动方向(f1)是向前上的,被邻牙所阻挡。如果按照图d所示,去除远中骨质(灰色部分)或切割牙体(r)后,旋转中心(O)下移,阻力点的运动方向就改变为向后上(f2),而得以避开邻牙阻挡而脱位。
1.3.2 转动轴、转动半径与差动
对于粗大、弯曲的 牙根,要消除脱位的阻力,可以通过设计转动轴心, 使得牙根在运动过程中,能顺着弯曲的牙槽窝而脱 位,这涉及转动半径与差动的原理,即在一个刚性 物体上某一点施加同样的力量,由于转动轴心的变 化,这一刚体其他点的运动方向将发生变化。牙根 脱位过程中,运动支点也就是运动轴心点的位置变 化,直接导致牙根受力时,转动半径的变化,并进 一步影响牙根根尖部位的运动方向和角动量,从而 使其易于脱位(图5、6)。
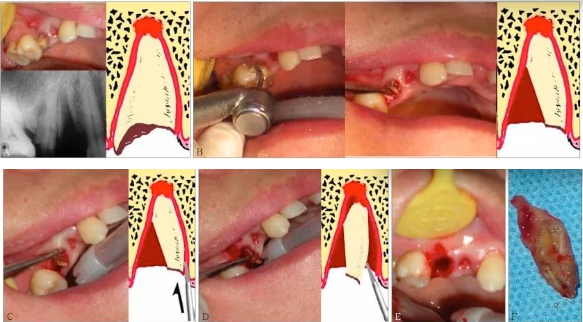
图 5 转动与差动
Fig 5 The rotation and the differential motion
A:口内(左上)和X线片(左下)见15残根,需拔除,右图为示意图;B:通过涡轮钻切割(左),挺除远中部分牙根(中)后,形成远中(凹面)低点的断面(右);C:在近中插入分离器械;D:牙根转动脱位;E:达成微创拔除的效果;F:拔除的牙根可见切割形成的断面。
2 力学原理在牙拔除术中应用的注意事项
上述力学原理在运用中仍需要结合具体情况, 灵活运用,毕竟在口内操作时,器械进入角度和深 度都会受到限制,牙根的变异也较大,故而在运用中,尚需注意以下几方面的问题和技巧。
2.1 剖牙的深度和角度
这个常常只能估算,但在估算中难免有偏差, 而这个偏差需要医生不断积累临床经验来获得。如图6所示的牙根,切割时应尽可能去除牙根最宽部位,以利于剩余牙根的活动。虽然可能通过制作导航件来解决此类问题,但为拔牙而设计一个导航件, 从时间和费用上考虑并不经济。
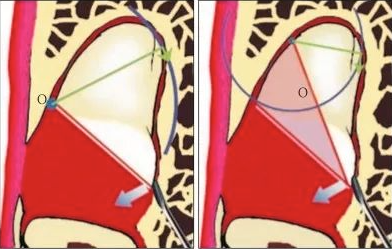
图 6 剖根的深度和差动
Fig 6 The depth of splitting and the differential motion
同样的牙根,剖根深度不同,根尖部位的运动方向将发生显著变化,从而导致牙齿脱位的阻力不同。左图中牙根脱位时,插入牙挺时,用力方向如蓝色箭头所示,牙根的运动轴心点是O,阻力点位置的运动方向(绿色箭头方向)受骨壁阻挡。而右图中牙根被进一步切割,运动轴心点(O)进一步下降,同样的阻力点的运动方向就变成了向上,避开了骨壁的刚性阻挡而得以脱位。
2.2 剖牙的部位和方向
随着锥形束CT的推广和普及,可以在术前就仔细分析阻力部位和方向,从而设计剖牙的部位和方向。
2.3 变向原理
因为解剖方位的限制,拔牙时器械多数是从前方进入的,并不能在每个拔牙的案例中实现理想的脱位根形,但上述原理可以帮助分析牙齿难以脱位的原因,而实际操作中,则可以通过变向的原理, 来达到较为轻松地脱位的微创效果(图7)。
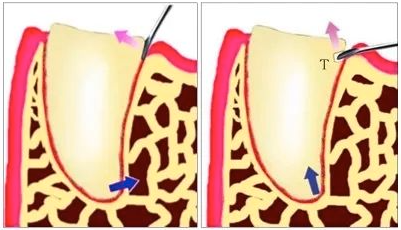
图 7 变向原理
Fig 7 The intentional change of dislocation direction
由于牙根的弯曲,使得正常方向(左图粉色箭头)用力会遇到较大阻力时,可以用涡轮钻在牙根的凹面上端制备沟槽(右图T),以器械采用挑拨的力量(右图粉色箭头),改变用力方向,而避开阻力。蓝色箭头指阻力点的运动方向。
免责声明:本文来源于网络,仅供医生学习交流,如有侵权,请联系删除!